a) What is a Stationary Point of a differentiable function of one variable? (2 marks)
View Solution
A stationary point of a differentiable function of one variable is a point (of the domain) of the function where the derivative is zero. Equivalently, the slope of the graph at that point is zero.
b) Renes Trading Company sells q kente strips per month at p Ghana Cedis per Kente strip. The demand function for kente strips is given by p=300−0.02q. The kente strips cost GH¢30 per strip to manufacture. There are fixed costs of GH¢9,000 per month.
Required:
i) Determine the price per kente strip that will maximize revenue. (4 marks)
View Solution
The demand function is given by p=300−0.02q
Thus the Total Revenue, TR(q) = (300−0.02q)q
The critical points of revenue is obtained by taking the derivative of TR(q)
Thus revenue is maximum at q=7500
Price that maximizes revenue is p=300=0.02(7500) = 150 GH₵
ii) Determine the quantity where profit is maximized. (4 marks)
View Solution
iii) Calculate the maximum profit. (2 marks)
View Solution
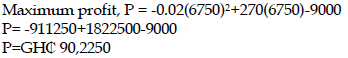
c) Due to changes in market conditions, the company finds the demand q, in thousands, for their kente strips to be 
at a price of GH¢p (p Ghana Cedis).
Required:
i) Determine the elasticity of demand when the price is GH¢5 and when the price is GH¢15 per kente strip. (6 marks)
View Solution
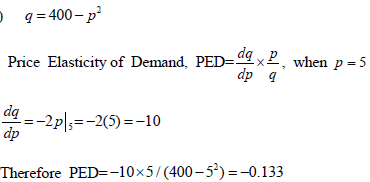
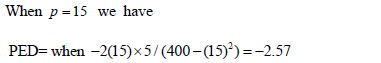
ii) Comment on your results in (i). (2 marks)
View Solution
It is inelastic at price 5 and elastic at 15.