Nov 2016 Q2

JinJin Company Limited makes two types of leather belts Type Superior and Type Standard. Type Superior is a highly quality and Type Standard is of lower quality. The respective profits are GHp 40 and GHp 30 per belt. The production of each of Type Superior requires twice as much time as a belt of Type Standard, and if all belts were of Type Standard, the company could make 1000 belts per day. The supply of leather is sufficient for only 800 belts per day (both Type Superior and Type Standard combined). Belt Type Superior requires a fancy buckle and only 400 of these are available per day. There are only 700 buckles a day available for belt Type Standard. If the aim is to determine how many units of the two types of belts the company should manufacture in order to have the maximum overall profit:

Required:
a) Formulate this problem as a Linear Programming Model.

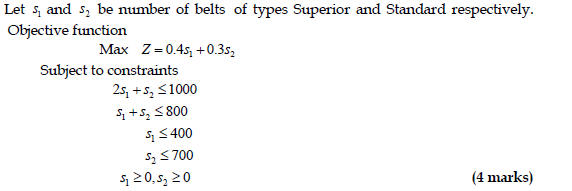
b) Set up the initial Simplex Tableau.                                                                                                                                 (4 marks)

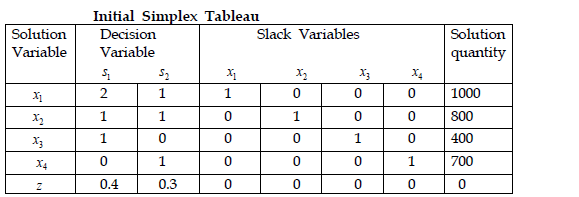
c) Solve your Tableau in (b) above.                                                                                                                                    (8 marks)

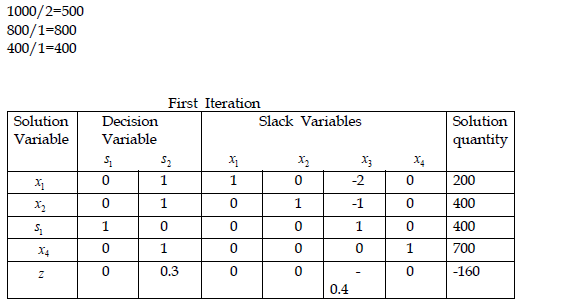
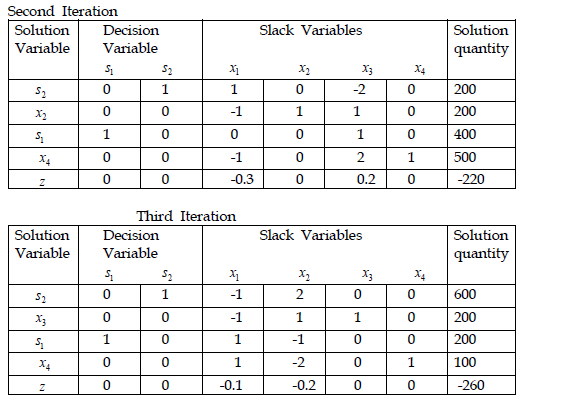
d) Interpret your final Simplex Tableau.                                                                                                                            (4 marks)